Möbius–Kantor polygon

In geometry, the Möbius–Kantor polygon is a regular complex polygon 3{3}3, , in . 3{3}3 has 8 vertices, and 8 edges. It is self-dual. Every vertex is shared by 3 triangular edges.[1] Coxeter named it a Möbius–Kantor polygon for sharing the complex configuration structure as the Möbius–Kantor configuration, (83).[2]

Möbius–Kantor polygon
Orthographic projection

shown here with 4 red and 4 blue 3-edge triangles.
Shephard symbol3(24)3
Schläfli symbol3{3}3
Coxeter diagram
Edges8 3{}
Vertices8
Petrie polygonOctagon
Shephard group3[3]3, order 24
Dual polyhedronSelf-dual
PropertiesRegular

Discovered by G.C. Shephard in 1952, he represented it as 3(24)3, with its symmetry, Coxeter called as 3[3]3, isomorphic to the binary tetrahedral group, order 24.

Coordinates

The 8 vertex coordinates of this polygon can be given in , as:

(ω,−1,0)(0,ω,−ω2)(ω2,−1,0)(−1,0,1)
(−ω,0,1)(0,ω2,−ω)(−ω2,0,1)(1,−1,0)

where .

As a Configuration

The configuration matrix for 3{3}3 is:[3]

Real representation

It has a real representation as the 16-cell, , in 4-dimensional space, sharing the same 8 vertices. The 24 edges in the 16-cell are seen in the Möbius–Kantor polygon when the 8 triangular edges are drawn as 3-separate edges. The triangles are represented 2 sets of 4 red or blue outlines. The B4 projections are given in two different symmetry orientations between the two color sets.

orthographic projections
Plane B4 F4
Graph
Symmetry [8] [12/3]

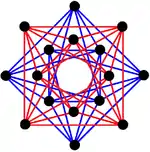This graph shows the two alternated polygons as a compound in red and blue 3{3}3 in dual positions.
3{6}2, or , with 24 vertices in black, and 16 3-edges colored in 2 sets of 3-edges in red and blue.[4]

It can also be seen as an alternation of , represented as . has 16 vertices, and 24 edges. A compound of two, in dual positions, and , can be represented as , contains all 16 vertices of .

The truncation , is the same as the regular polygon, 3{6}2, . Its edge-diagram is the cayley diagram for 3[3]3.

The regular Hessian polyhedron 3{3}3{3}3, has this polygon as a facet and vertex figure.

Notes
  1. Coxeter and Shephard, 1991, p.30 and p.47
  2. Coxeter and Shephard, 1992
  3. Coxeter, Complex Regular polytopes, p.117, 132
  4. Coxeter, Regular Complex Polytopes, p. 109

References
  • Shephard, G.C.; Regular complex polytopes, Proc. London math. Soc. Series 3, Vol 2, (1952), pp 82–97.
  • Coxeter, H. S. M. and Moser, W. O. J.; Generators and Relations for Discrete Groups (1965), esp pp 67–80.
  • Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974), second edition (1991).
  • Coxeter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.